高阶面试：伯努利过程

数据库 0 1057

小小草 2020年8月15日 11:17 发表

摘要：17世纪法国有个富二代叫洛必达，师从著名数学家约翰·伯努利。洛必达的愿望是成为一名数学家，但是天资不好，在班上成绩一直倒数。当听说老师伯努利正准备结婚但还差点钱时，他写了封信给伯努利表示想重金买他的论文，此时缺钱的伯努利笑开了花。论文发布后洛必达一夜成名，论文就是著名的《洛必达法则》。洛必达死后，伯

17世纪法国有个富二代叫洛必达，师从著名数学家约翰·伯努利。洛必达的愿望是成为一名数学家，但是天资不好，在班上成绩一直倒数。当听说老师伯努利正准备结婚但还差点钱时，他写了封信给伯努利表示想重金买他的论文，此时缺钱的伯努利笑开了花。论文发布后洛必达一夜成名，论文就是著名的《洛必达法则》。洛必达死后，伯努利觉得卖亏了，于是把当时的交易信息公布出来，但命名已无法改回。当下每天都有人在课堂上悼念洛必达，不过今天的主角是伯努利。

伯努利家族的发家史是扔骰子和抛硬币，在统计学、概率学、数学上做出了突出的贡献。今天要讲的内容就是著名的《伯努利过程》。

题目：如果你是淘宝直播的研发，如何实时显示观看直播的总人数？

基数

基数（cardinality，也译作势），是指一个数据集中不同元素的个数。例如集合 {1,2,3,1,2} 的基数是3（去重后的个数）。工作中我们常常需要统计网站UV、App日活、微博与朋友圈点赞数、QQ空间访问量、直播观看人数等，都属于基数统计。

一般会用集合统计基数，集合的算法很容易实现，但是特别耗内存。比如李佳琦有一亿多粉丝，使用集合会消耗1G 左右的内存。要是有一千个李佳琦这样的大咖用此功能，会消耗1T内存，一百万主播来用会让整个阿里破产。

另一种方案是用Bitmap统计基数，统计一亿粉丝会消耗12.5M内存，一千个李佳琦这样的大咖需要 12.5G 内存。相比上一种方案优化了不少，但是淘宝直播有几百万主播需要此功能，消耗的总内存会超过10T。这种方案会让淘宝直播团队破产。

PS：Bitmap是使用一个很长的bit数组表示集合，将bit位顺序编号，bit为1表示此编号在集合中，为0表示不在集合中。例如"00100110"表示集合 {2，5，6}，Bitmap中1的数量就是这个集合的基数。

基数估值算法

为了不让淘宝直播破产，P7程序员使用HLLC算法来实现此功能。HLLC算法对粉丝数量没有限制，每个主播会消耗5byte - 12Kb内存。一百万主播消耗 5MB-12GB 的内存。因为大部分主播的粉丝数不多，压缩数据后一百万主播的真实内存消耗会在4G左右，这点费用可以忽略不记。唯一的问题是HLLC得到的是估值，标准误差为0.81%。比如真实访问量是10000，计算的结果可能是9919~10081。和内存费用比一下这点误差完全可以接受。

HLLC算法已经非常成熟，比如Redis中已经集成了该算法 HyperLogLog。GitHub上也有各个语言的实现方案。如果只是实现此功能看到这里就行了。如果是参加面试，肯定会被追问，请继续阅读。

伯努利实验

抛一枚公平的硬币1次，结果只有两种可能，正面朝上或者背面朝上。正面（国徽）朝上的概率是50%，背面朝上的概率也是50%。

一个数学题：N个人分别抛硬币，抛到正面就淘汰，最后剩下的一人胜出。如果最后胜出的人一共抛了6次硬币，请估算N是多少？

我们用1表示正面，0表示背面，那么赢家抛硬币的结果是「000001」。N个人表示进行了N次伯努利过程。图如下：

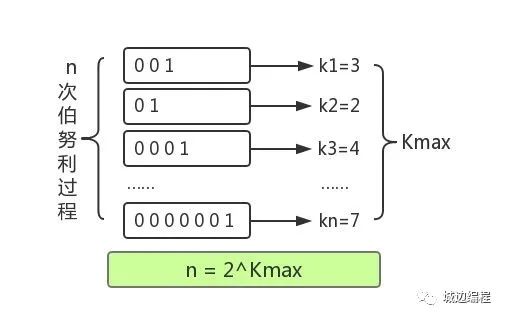
K是每回合抛到1所用的次数，我们已知的是最大的K值，用Kmax表示。由于每次抛硬币的结果只有0和1两种情况，因此，Kmax在任意回合出现的概率即为(½)Kmax ，进一步得出 N*(½)Kmax = 1 ,因此可以推测 N=2kmax 概率学把这种问题叫做伯努利实验。通过公式我们可以估算出 N = 2^6 = 64。

通过这个数学问题我们会发现这是一种通过局部信息预估整体数据的方法。尝试应用到访问量计算中，每当有用户访问，我们就循环运行概率为50%的随机函数，比如 `random(0,1)`，当函数返回1时表示抛到了正面，并记录循环次数。伪代码如下：

bit array[64] = [0];
int i=0;
while(true){
    i++;
    int r = random(0,1);
    if(r==1){
        array[i] = 1;
        i=0;
        break;
    }
}

最后找到bit数组中最末尾1的位置，然后通过公式 `N=2^kmax`得到访问量N。到这里整个思路完全讲清楚了，但是得到的值标准误差会很大，而且random()函数循环运行的效率也很低。下面看Redis是如何优化的。

Redis中的HyperLogLog

Redis中实现HyperLogLog的方式可以理解为优化`random()`函数和bit数组。

优化 random()：HyperLogLog对原始数据（比如访客id）做6次hash得到6个64位比特串（8byte），相当于一个BIGINT。因为hash函数并非绝对的均匀分布，所以增加6个不同的hash函数减少误差。

优化bit数组：HyperLogLog 一共创建了 2^14 个桶（16384）。每个桶中是一个 6 bit 的数组，约12KB。这样做可以减少内存使用并且减少误差。

实现方式：将64位比特串的低 14 位单独拿出，它的值就对应桶的序号。将剩下 50 位中第一次出现 1 的位置值设置到桶中。在设置前，要判断进桶的值是否大于桶中的旧值，如果大于才进行设置，否则不进行设置。最后通过对所有桶取调和平均再加上其他优化算法得到总数N。

Redis还做了大量的优化细节，比如使用内存压缩算法，当用户访问量少时会使用稀疏存储，内存消耗可缩减到5byte。使用调和平均数来代替几何平均数，降低离群值对结果的影响。算法支持并行化，比如6个散列函数可以并行计算，16384个桶可以并行计算之后合并，并不影响最终结果。

最后

通过局部信息预估整体数据的方法其实并不复杂，但是会打开一扇门，让人眼前一亮。最近写文章都是逼着自己在写，作为奔三的程序员随着年龄的增长最怕的不是被淘汰，而是怕变的平庸，平庸这东西犹如白衬衣上的污痕，一旦染上便永远洗不掉，无可挽回。

转自：https://my.oschina.net/u/3573857/blog/4493276

点赞 0 收藏(0)